SolidShapesSurfaceAreaAndVolume.solution

1. Three metallic solid cubes, whose edges are 3 cm, 4cm, and 5cm, are melted and formed into a single cube. Find the edges of the cube so formed.

Sol.  Here , edge of there metallic cubes are 3 cm, 4cm, and 5cm.

Volume of single cube = 33+43+53

= 27 +64 +125

= 216 cm3

 Therefore,edgeofsinglecube=216−−−√3=6

2. The rainwater from a roof of dimensions 22 m * 20m drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m. If the rainwater collected from the roof just fill the cylindrical vessel, then find the rainfall in cm.

Sol. Let the required rainfall in cm be x

therefore according to the statement of the question, we have

Volume of rain = volume of cylinder

 x100×22×20=227×1×1×3.5

x= 227×1×1×3.5×10022×20

=2.5m

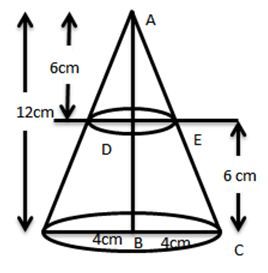
3. A cone having radius 8 cm and height 12 cm is divide into two part by a plane through the mid-point of axis parallel to its base. Find the ratio of the volumes of two parts.

Sol.   Here,   △ADE∼△ABCbyAAsimilarityruler4=612

∴radiusofsmallerconeradiusoflargercone=HeightofsmallerconeHeightoflargercone

⇒ r=2cm

now,volumeofupperpart(cone)volumeoflowerpart(frustumofcone)

=13πr2h13πh(r2+R2+R)

=2×2×66(4+16+8)

=428

=17

So that required ratio is 1:7.

4. Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water. Find the number of marble that should be dropped into the beaker so that the water level rises by 5.6 cm.

Sol. Let us assume that the marbles are spherical in shape,

Hence,Volume of each marble

=43×π×0.7×0.7×0.7

Let n be the number of marbles that are required to raise the water  level  upto 5.6cm of the cylindrical beaker

 therefore n times volume of each marble = Volume of cylindrical beaker of height 5.6cm.

n×43×π×0.7×0.7×0.7 =π×72×72×5.6

n=72×72×5.6×34×10.7×10.7×10.7

n= 150.

5. Find the number of metallic circular disc with 1.5 cm base diameter and of height 0.2 cm. to be melted to from a right circular cylinder of diameter 4.5 cm and height 10 cm.

Sol.         Volume of each circular disc

=π×1.52×1.52×0.2cm3

Volume of right circular cylinder

=π×4.52×4.52×10cm3

Let the number  of metallic circular disc be n

∴n×Volumeofeachcirculardisc=Volumeofcylinder

∴n×π×1.52×1.52×0.2=π×4.52×4.52×10

n=4.52×4.52×10×21.5×21.5×10.2

=450

6. A heap of rice is in the form of a cone of diameter 9 m and height 3.5 m. find the volume of the rice. How much canvas cloth is required to just cover the heap?

Sol. Radius of conical heap of rice (r) = 92=4.5m

Height of conical heap of rice (h) = 3.5m

Therefore, Volume of the rice =13×π×r2×h

=13×227×4.5×4.5×3.5

=74.25 m3

Therefore the Slant height of the heap =(4.5)2+(3.5)2−−−−−−−−−−−−√

=20.25+12.25−−−−−−−−−−−√

=32.5−−−−√=5.7m

Area of the canves cloth required  =227×4.5×5.7

=80.6m3

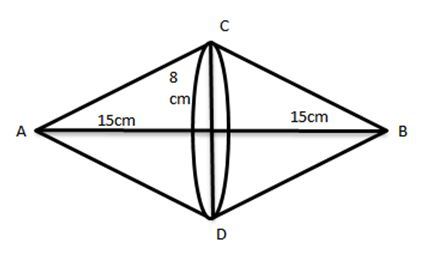
7. Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape so formed.

Sol.

Slant height of cone  = 82+152−−−−−−−√

=64+225−−−−−−−√

=289−−−√

=17cm

Total surface area of the shape so formed

= 2×Curvedsurfaceoftheoriginalconeused

=2×227×8×17

=854.86cm2

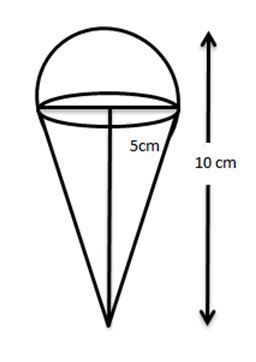
8. An ice-cream cone full of ice cream having radius 5cm and height 10cm as shown in the figure. Calculate the volume of ice-cream, provided that its 16 part is left unfilled with ice-cream.

Sol.  Radius of the cone (r)  = 5cm

Total height of ice-cream cone = 10cm

Height of cone = 10 – 5=5cm

Volume of the ice-cream = 13πr2h+23πr3

=13πr2(h+2r)

=13×227×25(5+10)

=13×227×25×15

=392.86cm3

Volume of ice-cream = (1−16)of392.86

=56×392.86

=327.38cm3

9. How many spherical lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimensions 66cm, 42cm, and 21cm?

Sol.  Let n be the number of spherical lead shots.

n×volumeofeachsphericalleadshot=volumeoftherectangularleadpiece

n=43×227×4.22×4.22×4.22=66×42×21

=×66×42×21×3×7×84×22×4.2×4.2×4.2

=1500

Hence, the required number of spherical lead shots are 1500.

10. A well 24m long, 0.4m thick and 6m high is constructed with the bricks each of dimensions 25cm×16cm×10cm. IF the motor occupies 110  th of the well, then find the number of bricks used in constructing the well.

Sol.       Volume of the wall = 24m×0.4m×6m

=2400×40×600cm3

=57600000cm3

Volume of the wall occupied by motor = 110×5700000

=5760000cm3

Volume of the wall constructed with bricks = 57600000−5760000cm3

=51840000

Let n be the number of bricks required

∴n×25×16×10 =51840000

⇒n=5184000025×16×10=12960

11. A solid metallic hemisphere of radius 8 cm is melted and re-casted into a right circular cone of base radius 6 cm. Determine the height of the cone.

Sol.   Let h be the height of the cone.

Volume of the cone  = Volume of hemisphere

13πr2h=23πr3

⇒6×6×h=2×8×8×8

h=2×8×8×86×6

h= 28.44

Hence, the height of cone is 28.44cm

12. How many cubic centimeters  of iron is required to construct an open box whose external dimension are 36 cm, 25cm  and 16.5 cm provided the thickness of the iron  weights 7.5g, Find the weight of the box.

Sol.  The Volume of the external box =  36×25×16.5

=14850

Volume of the internal box=33×22×15

=10890cm3

Therefore length =36-1.5-1.5 =33cm

breadth  =  25-1.5-1.5 =22cm

Height =16.5-1.5 =15cm

Volume of  iron used =14850-10890

=3960 cubic cm

Weight of the box = 3960×7.5

=29700g

=29.7kg

13. Water flows at the rate of 10m/ minute through a cylindrical pipe 5 mm in diameter. How long would it take to fill a conical vessel whose diameter at the base is 40cm and depth 24 cm?

Sol. Radius of cylindrical pipe =52mm

=52cm

Length per min = 10m

=1000cm

 thereforeVolumeofwaterflowingperminute=πr2h

=227×520×520×1000

Here, Radius of the conical vessel = 20cm

Depth of the conical vessel =24cm

Now Volume of the conical vessel=13×227×20×20×24

Therefore Time required to the conical vessel

=13×227×20×20×24227×520×520×1000

=51minutes 12 second

14. A factory manufactures 120000 pencils daily. All pencils are cylindrical in shape each of length 25cm , circumference of base as 1.5cm. Determine the cost of coloring the curved surface of the pencils manufactured in one day at the rate of 0.05 per dm3.

Sol.  Given that, Circumference of base of pencil =1.5cm

2πr=1.5cm

r=1.52πcm

So, Curved surface area of each pencil =2π×1.52π×25

=37.5cm2

Total Curved surface area of 120000 pencils

=0.375×120000=45000dm2

Total cost of coloring the C.S.A is 120000 pencils

=0.05×45000=2250

15. water is following at the rate of 15 km/h through a pipe diameter 14cm, a cuboidal pond which is 50 m long and 44m wide. IN what time will the level of water in pond rise by 21cm?

Sol. Hence, Volume of the pound =×50m×44m×21100m

=462m3

Radius of pipe (r) =142×1100

=0.07m

Length of the pipe per hour= 15km

=15000m

Therefore Water collected per hour =227×0.07×0.07×15000

=231m3}

Time required to rise the water level by 21cm

=462231

=2hours

16. A milk container of height 16cm is made of metal sheet in the from of a frustum of a cone with radii of its lower and upper ends as 8cm and 200cm 22 Rs. per liter which the container canhold.

Sol. Height of the frustum of cone(h)= 16 cm

Radii of lower and upper end are

R=8cm and R = 20cm

Therefore Volume of the milk =13πh(R2+r2+Rr)

=13×227×16(202+82+20(8))

=22×1621×(400+64+160)

=22×1621×624

=10459.43cm3

=10459.431000litres

=10.459litres

Total cost of the milk =22×10.459Rs

=230.10Rs

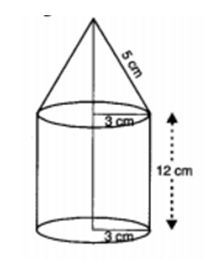
17. A rocket is in the from of a right circular cylinder close at the lower end surmounted by a cone with the same radius as that of the cylinder .The diameter and height of the cylinder are 6cm and 12 cm respectively. If the slant height of the conical portion is 5cm, find the total surface area and volume of the rocket. [use π=3.14]

Sol.         Height of the cone =52−32−−−−−−√

=25−9−−−−−√=16−−√=4