AreaRelatedToCircles.solution
⇒ Radius = 82 = 4 cm
⇒ πR21+πR22=πR2
⇒ R21+R22=R2 or R = R21+R22−−−−−−−√
⇒ 2πR1+2πR2=2πR
⇒ R1+R2=R
⇒ 2πr=4×side
⇒ r=2π×side
⇒ πR2=π(4)2+π(3)2
⇒ πR2=π(16+9)
⇒ R2=25
⇒ R = 5 m.
⇒ Diagonal of square = Diametre of circle
⇒ 2–√×side = 12
⇒ R=R1+R2
⇒ R = 12 + 8 = 20 cm
πR2=πR21+πR22
⇒ R2=R21+R22
⇒ R2=(20)2+(15)2 = 400 + 225 = 625
⇒ R = 25 cm
⇒ 2–√×side = 14
⇒ side = 142√ cm
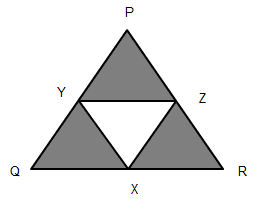
∠P=∠Q=∠R=60°
⇒r=22×7×360°60°×2×22 = 21 cm
⇒θ360°×2×227×7 = 4
⇒θ360° = 4×72×22×7 = 111
πr2 = 1.32
r2 = 1.32×722 = 0.42
1. If perimeter of a circle is equal to that of a square, What would be the ratio of their areas.
Here, perimeter of circle = 2πr and perimeter of square = 4a
∴2πr = 4a ⇒r=2aπ
∴ Ratio of their areas = πr2a2 = πa2×(2aπ)2
= πa2×(4a2π2) = 4π = 422×7 = 1411
2. Find the areas of circle that can be inscribed in a square of side 8 cm.
Diameter of the circle = Side of the square
∴ Diameter = 8 cm
∴ Area of the circle = π×4×4 cm2
= 16π cm2
3. If sum of the areas of two circles with radii R1andR2 is equal to area of a circle radius R, derive the relation among their radii.
Since sum of areas of two circles with radii R1andR2 = Area of circle with radii R.
4. If sum of the circumference of two circles with radii radii R1andR2 is equal to circumference of a circle radius R, derive the relation among their radii.
Since sum of circumference of two circles with radii R1andR2 = Circumference of circle with radii R.
5. If the circumference of a circle and the perimeter of a square are equal, then write the relation between their radii.
Since sum of circumference of a circle = Perimeter of a square
∴ Area of circle = π×4π2×(side)2
= 4π(side)2
= 2822(side)2
Area of square = (side)2
Since 2822(side)2 > (side)2
6. To build a single circular park equal in area to the sum of areas of two circular parks of diameter 8 m and 6 m in a locality. What would be the radius of new park?
Here, area of single park = Area of the park with (d= 8m) + Area of the park with (d= 6m)
7. Find the area of a square that can be inscribed in a circle of radius 6 cm.
Since square is inscribed in a circle
Side = 122√ cm
Now, area of the square = 122√×122√ = 72 cm2
8. Find the radius of a circle whose circumference is equal to the sum of the circumference of two circles of diameter 24 cm and 16 cm.
From the above, we obtain
2πR=2πR1+2πR2
9. Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 20 cm and 15 cm.
From the above, we obtain
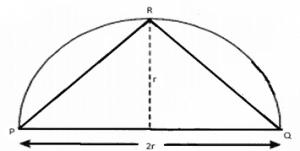
10. Find the area of the largest triangle that can be inscribed in a semicircle of radius r.
Here, among all altitudes, radius is the largest altitude

∴ Areaof△PQR=12×2r×r
= r2sq.units
Hence, area of the largest triangle inscribed in a semicircle r is r2sq.units .
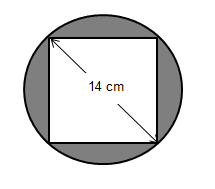
11. In the given figure , a square of diagonal 14 cm is inscribed in a circle. Find the area of the shaded region.

Here, diagonal of the square = 14 cm
∴ Area of the square = 82√×82√ = 98 sq.cm
Diameter of the circle = 14 cm
∴ Radius of the circle = 7 cm.
Area of the circle = π(4)2 = 227×49 = 154 sq.cm
Thus, area of the shaded region = 154 – 98
= 56 sq.cm
12. The wheel of a motor cycle is of radius 28cm. How many revolutions per minitue must the wheel make so as to keep a speed of 60 Km/h?
Here, speed of the motor cycle = 60 Km/h
= 6000060 m/min
= 1000 m/min
Radius of the wheel (r) = 28 cm = 28100 m.
Circumference of the wheel = 2×227×28100 m
= 1.76 m
Number of revolutions per minute = 10001.76
= 568.18
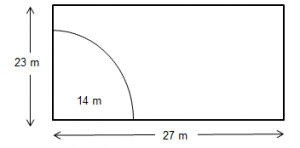
13. A cow is tied with a rope of length 21 m at the corner of a rectangular field of dimensions 27 m × 23 m. Find the area of the field in which the cow can graze.
Length of the rope = 21 m
∴ Area of the field in which the cow can graze

= 90°360°×227×21×21
= 346.5 m2
14. In the given fig, arcs are drawn by taking vertices P,Q and R of an equilateral triangle of side 12 cm to intersect the sides QR, RR and PQ at their respective mid-points X, Y and Z. Find the area of the shaded region.
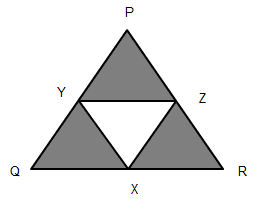
Side of an equilateral m2△ PQR = 12 cm
Since, arcs are drawn by taking vertices P,Q and R to intersect the sides QR, RR and PQ at their mid-points X, Y and Z.
∴ Radii of each sector (r) = 6 cm
Also, m2△ PQR is an equilateral, therefore
Required area of the shaded region
= 3×θ360°×πr2
= 3×60°360°×3.14×62
= 3×16×3.14×36
= 56.52 cm2
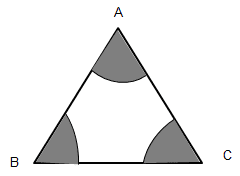
15. In the given fig, arcs have been drawn with radii 7 cm each and with centers A, B and C.
Find the area of the shaded region.

Here, radii of each sector at A, B and C is 7 cm
Let ∠A=θ1°∠B=θ2°,∠C=θ3°
Required area of shaded region
= θ1°360°πr2+θ2°360°πr2+θ3°360°πr2
= πr2360°(θ1°+θ2°+θ3°)
= 22×7×77×360°×180° [Sinceθ1°+θ2°+θ3°=180°]
= 77 cm2
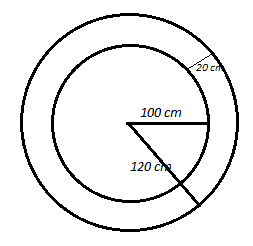
16. A circular park is surrounded by a road 20 m wide. If the radius of the park is 100 m, find the area of the road.

Here, radius of the circular park (r) = 100 m
Width of the road = 20 m
∴ Radius of the outer circle (R) = 100 + 20 = 120 m
Required area of road
= πR2+πr2
= π (R + r) (R – r)
= 227 (120 + 100) (120 – 100)
= 227×220×20 = 13816 m2
17. A piece of wire 22 cm long is bent into the form of an arc of a circle subtending an angle of 90° at its center. Find the radius of the circle.
Here, length of wire (arc of required circle) = 22 cm
And central angle(θ ) = 90°
Let r be the radius of the required circle.

∴θ360°×2πr = length of the arc
∴60°360°×2×227r = 20
18. The length of the minute hand of a clock is 7 cm. Find the area swept by the minute hand during the time period 6:05 A.M and 6:40 A.M.
Angle swept by the minute hand in one minute = 6°
∴Angle swept by the minute hand in 35 minute = (6×35)°=210°
Length of the minute hand = 7 cm
Area swept by the minute hand = 210°360°×227×7×7
= 89.83 cm2
19. Find the area of the sector of a circle of radius 7 cm, if the corresponding arc length is 4 cm.
Radius of the circle (r) = 7 cm
Length of the arc = 3.5 cm
∴ θ360°×2πr = 4 cm
Now, area of the corresponding arc
= 111×227×7×7
= 14 cm2
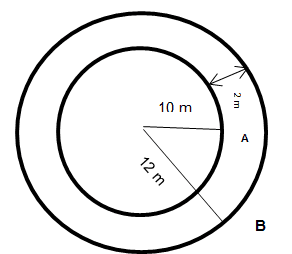
20. A circular pond is of diameter 20 m. It is surrounded by a 2 m wide path. Find the cost of constructing the path at the rate of Rs.30 per m2 .
Radius of the circular pond r = 202 = 10 m
Width of the path = 2 m

∴ Radius of the outer circle (R) = 10 + 2 = 12 m
Area of the path = πR2−πr2
= π (R + r) (R – r)
= 227 (12 + 10) (12 – 10)
= 227×22×2 = 138.16 m2
Cost of constructing the path @ Rs.30 per m2
= Rs.4144.8
21. Find the number of revolutions made by a circular tier of area 1.32 m2 in rolling a distance of 165 m.
Area of a circular wheel = 1.32 m2
r = 0.42−−−−√ = 0.648 m
Distance traveled in one rotation = 2πr
= 2×227×0.648
= 4.07 m
Total distance to be travelled = 165
∴Number of rotations = 1654.07 = 40.54
No comments:
Post a Comment