EXERCISE – 4.1
x2−(3–√+2–√)x+6–√ = 0
x2−3–√x−2–√x+6–√=0
x(x−3–√)−2–√(x−3–√)=0
(x−3–√)(x−2–√)=0
10x2−73–√x+3=0
10x2−73–√x+3=0
x2−73√x10+310=0
x2−(3√2+3√5)x+310=0
x2−3√2x−3√5x+310=0
x(x−3√2)−3√5(x−3√2)=0
(x−3√2)(x−3√5)=0
x2−110x+1400=0
x2−(120+120)x+1400=0
x2−120x−120x+1400=0
x(x−120)−120(x−120)
(x−120)(x−120)
3–√x2+7x+23–√=0
3–√x2+7x+23–√=0
x2+73√x+2=0
x2+63√x+13√x+2=0
x(x+63√)+13√(x+23–√)=0
(x+13√)(x+23–√)=0
x=2+12−−√ or x=2−12−−√
(2x)2+2(2x.12)=8
(2x)2+2(2x.12)+14=8+14
(2x+12)2−(334−−√)2=0
(2x+12+33√2)(2x+12−33√2)=0
x+1x=5 , with x ≠ 0.
x=−(−5)+(−5)2−4(1×1)√2×1 and x=−(−5)−(−5)2−4(1×1)√2×1
x=5+25−4√2 and x=5−25−4√2
x=5+21√2 and x=5−21√2
1x−1x−3=7 , where x≠0,3
x=−(−21)+(−21)2−4(7×3)√2×7 and x=−(−21)−(−21)2−4(7×3)√2×7
x=21+441−84√14 and x=21−441−84√14
x=21+357√14 and x=21−357√14
Exercise 4.2
Q1. Find the roots of quadratic equation by factorization:
Sol.
Therefore x=2–√ or x=3–√
Q2. Find the roots of quadratic equation:
Sol.
Therefore x=3√2 or x=3√5
Q3. Find the roots of quadratic equation:
400x2 – 40x + 1 = 0
Sol.
Since, 400x2 – 40x + 1 = 0
Therefore, x2−110x+1400=0
Therefore x=120 or x=120
Q5. Find the roots of quadratic equation:
Sol.
Therefore x=−13√ or x=−23–√
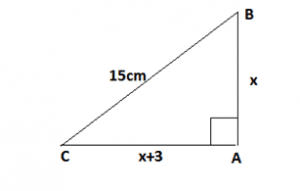
Q.8 The base of a right angled triangle is 3cm more than its altitude. If the hypotenuse is 15cm. Find the length of its base and altitude.
Sol.
In right angled triangle ABC:

Let, length of altitude = x cm
Therefore base = (x + 3) cm
oth LHS and RHS, we get the following equation:-
x2 – 2(2x) + 22 = 8 +22
(or), (x – 2)2 = 12
(x – 2)2 = 12−−√
(x – 2)2 – (12−−√)2 = 0
Since, a2−b2=(a+b)(a–b)
Therefore, (x−2−12−−√) (x−2+12−−√)
This is how we find roots of a given equation by method of completing the square.
Exercise – 4.3
Q.4 Find the roots of the equation 2x2 + x – 4 = 0 by method of completing the square.
Sol.
Therefore,
4x2 + 2x = 8
Now,
Therefore x=−1+33√4 or x=−1+33√4
Exercise 4.4
Q.1 Find the roots of following equation:
Sol.
On simplifying the above equation we get:
x2 – 5x + 1 = 0
Here, a=1, b = – 5 and c = 1.
On putting the values of a, b and c in quadratic formulae we get:
Q.2 Find the roots of following equation:
Sol.
On simplifying the above equation we get:
7x2 – 21x + 3 = 0
Here, a = 7, b = -21 and c = 3
On putting the values of a, b and c in quadratic formulae we get:
Q.4 Find the values of k in the following quadratic equation so that they have two equal real roots 3x2 + kx + 5 = 0
Sol.
Given, 3x2 + kx + 5 = 0
Here a = 3, b = k and c = 5
Sol.
Here a = 2, b = 1 and c = – 4
Since,
D = b2 – 4ac
Therefore,
D= 12 – 4(- 4 × 2)
D= 1 + 32
Therefore, D= 33
Since, D > o. The given quadratic equation will have real roots.
No comments:
Post a Comment