PairOfLinearEquation.solution

Exercise 1 

Question 1:

Astitva tells his daughter, “Seven years ago I was seven times as old as you were then and also three years from now, I shall be three times as old as you will be.”  Represent this situation algebraically and graphically.

Solution:

Let the present age of Astitva be ‘x’.

And, the present age of his daughter be ‘y’.

Seven years ago,

Age of Astitva = x-7

Age of his daughter =y-7

According to the question,

x−7=7(y−7)

⇒x−7=7y−49

⇒x−7y=−42         ………………………(i)

Three years from now,

Age of Astitva will be ‘x+3’

Age of his daughter will be ‘y+3’

According to the question,

x+3=3(y+3)

⇒x+3=3y+9

⇒x−3y=6       …………………(ii)

Subtracting equation (i) from equation (ii) we have

(x−3y)−(x−7y)=6−(−42)

−3y+7y=6+42

⇒4y=48

⇒y=12

The algebraic equation is represented by

x−7y=−42

x−3y=6

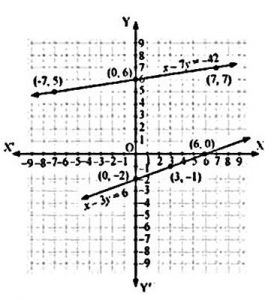
For x−7y=−42

x=−42+7y

The solution table is

X	-7	0	7
Y	5	6	7

For  x−3y=6   or     x=6+3y

The solution table is

X	6	4	0
Y	0	-1	-2

The graphical representation is-

Question 2:

A cricket team coach purchases 3 bats and 3 balls for Rs 3900. Later on, he buys 1 bat and 2 more balls of the same kind for Rs 1200. Represent the situation algebraically and geometrically.

Solution:

Let us assume that the cost of a bat be ‘Rs x’

And,the cost of a ball be ‘Rs y’

According to the question, the algebraic representation is

3x+6y=3900

x+2y=1300

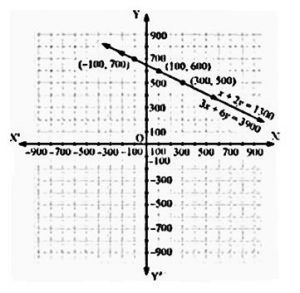
For 3x+6y=3900

x=3900−6y3

The solution table is

x	300	100	-100
y	500	600	700

For,

x+2y=1300

x=1300−2y

The solution table is

x	300	100	-100
y	500	600	700

The graphical representation is as follows.

Question 3:

The cost of 2 kg of apples and 1 kg of grapes on a day was found to be Rs 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is Rs 300. Represent the given situation algebraically and geometrically.

Solution:

Let the cost of 1 kg of apples be ‘Rs x’

And, cost of 1 kg of grapes be ‘Rs y’

According to the question, the algebraic representation is

2x+y=160

4x+2y=300

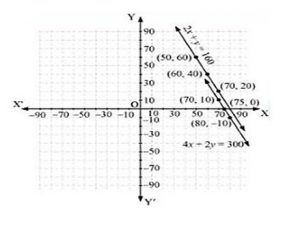
For,  2x+y=160

y=160−2x

The solution table is

X	50	60	70
Y	60	40	20

For 4x+2y=300,

y=300−4x2

The solution table is

x	70	80	75
y	10	-10	0

The graphical representation is as follows.

Exercise-2

Question 1: 

Find the graphical solution for the given problems.

 (a).In Class 10th, 10 students participated in a Maths test. If there are 4 more girls than the total number of boys, find how many girls and boys participated in the test.

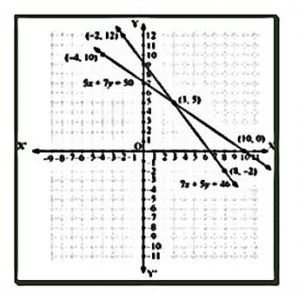
(b)The total cost of 5 erasers and 7 chocolates is Rs.50, but the total cost of 7 erasers and 5 chocolates is  Rs. 46. Now, calculate the cost of one eraser and the cost of one chocolate.

Solution:

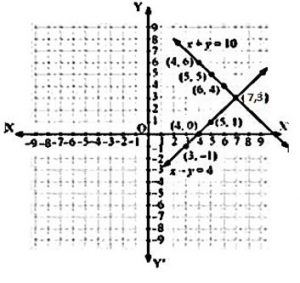
(a)Let there are x number of girls and y number of boys. As per  the given question,  it is represented as follows.

x+y=10x−y=4Nowx+y=10,x=10−y

X	5	4	6
Y	5	6	4

Forx−y=4,x=4+y

X	4	5	3
Y	0	1	-1

Hence, the table is represented in graphical form as follows.

From the figure, it is seen that the given lines cross each other at point (7, 3). Therefore, there are 7 girls and 3 boys in the class .

(b)Let 1 pencil costs Rs.x and 1 pen costs Rs.y. According to the question, the algebraic representation is

5x+7y=507x+5y=46For5x+7y=50, x=50−7y5

x	3	10	-4
y	5	0	10

7x+5y=46

X	8	3	-2
Y	-2	5	12

Hence, the graphic representation is as follows.

From the figure, it is seen that the given  lines cross each other at point (3, 5).

So, the cost of a eraser is 3/- and cost of a chocolate is 5/-.

Question 2:

Comparing the given ratios, a1a2,b1b2andc1c2,Figure out whether the lines are parallel or coincident:

(a) 5x−4y+8=0

7x+6y−9=0

(b) 9x+3y+12=018x+6y+24=0

(c) 6x−3y+10=02x−y+9=0

Solution:

(a) 5x−4y+8=0

7x+6y−9=0

Comparing these equations with a1x+b1y+c1=0

and a2x+b2y+c2=0

We get,

a1=5,b1=−4,c1=8a2=7,b2=6,c2=−9

a1a2=57

b1b2=−46=−23

Since a1a2≠b1b2

So, the pairs of equations given in the question have a unique solution and the lines cross each other at exactly one point.

(b) 9x+3y+12=018x+6y+24=0

Comparing these equations with a1x+b1y+c1=0

and a2x+b2y+c2=0

We get,

a1=9,b1=3,c1=12a2=18,b2=6,c2=−24

a1a2=918=12

b1b2=36=12

c1c2=1224=12

Since a1a2=b1b2=c1c2

So, the pairs of equations given in the question have infinite possible solutions and the lines are coincident.

(c) 6x−3y+10=02x−y+9=0

Solution: Comparing these equations with a1x+b1y+c1=0

and a2x+b2y+c2=0

We get,

a1=6,b1=−3,c1=10a2=2,b2=−1,c2=9

a1a2=62=31

b1b2=−3−1=31

c1c2=109

Since a1a2=b1b2≠c1c2

So, the pairs of equations given in the question are parallel to each other and the lines never intersect each other at any point and there is no possible solution for the given pair of equations.

Question 3:

Compare the given ratios, a1a2,b1b2andc1c2 find out whether the following pair of linear equations are consistent, or inconsistent.

(a) 3x+2y=5;2x−3y=7

(b) 2x−3y=8;4x−6y=9

(c) 32x+53y=7;9x−10y=14

Solution:

(a) 3x+2y=5;2x−3y=7

a1a2=32

b1b2=−23

c1c2=57

Since a1a2≠b1b2

So, the given equations intersect each other at one point and they have only one possible solution. The equations are consistent.

(b) 2x−3y=8;4x−6y=9

a1a2=24

b1b2=−3−6

c1c2=89

Since a1a2=b1b2≠c1c2

So, the equations are parallel to each other  and they have no possible solution. So, the equations are inconsistent.

(c) 32x+53y=7;9x−10y=14

a1a2=329=16

b1b2= frac53−10=−16

c1c2=714

Since a1a2≠b1b2

So, the equations are intersecting  each other at one point and they have only one possible solution. So, the equations are consistent.