ApplicationsOfTrignometry.solution
⇒∠PRQ=90°−θ
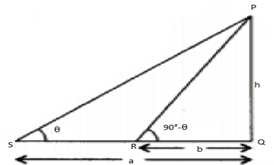
ha=tan θ
hb=tan(90°−θ) = cot θ
h2 = ab tan θ cot θ = ab
⇒h=ab−−√
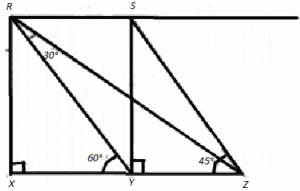
∠YRS=∠XYR (alternative.int. ∠a )
⇒∠YRS = 60°
⇒∠ZRS+∠YRZ=60°
⇒∠ZRS+30°=60°
⇒∠ZRS=30°
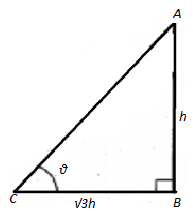
⇒ θ = 30°
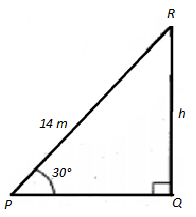
QRPR = sin 30°
h14=2√2
RTAT = tan θ
20.820.8 = tan θ
θ =45°
PQAQ = tan 45°
⇒ PQAQ = 1
⇒ PQ = AQ= h m
PQBQ = tan 60°
PQBQ = 3–√
hh−100 = 3–√
(3–√−1)h = 3–√(100)
RYSY = tan 60°
⇒ RYSY = 3–√
⇒ h = 3–√ SY
RXSX = tan 30°
⇒ RXXY+YS = 13√
⇒ h40+YS = 13√
⇒ 3–√ h = 40 + YS
⇒ 3–√ h = 40 + h3√
∠RXS = γ , ∠RYS = δ
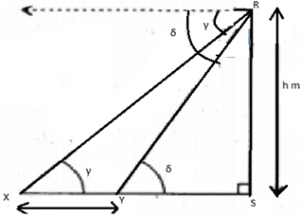
RSYS = tan δ
⇒ RS = YS tan δ …..(i)
RSXS = tan γ
⇒ RSXY+YS = tan γ
⇒ RS = (XY+YS) tan γ …..(ii)
⇒ htanγ = XY + RStanδ [using (i)]
⇒ h cot γ = XY + h cot δ
⇒
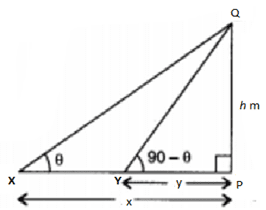
PQPX = tan θ
hx = tan θ
PQPY = tan (90°−θ)
hy = cot θ
h2 = x tan θ ×y×1tanθ = xy
∠SPR=30°and∠SQR=45° .
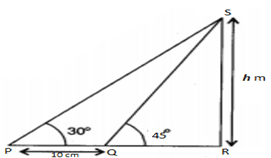
SRQR = tan 45°
⇒ SR = QR = h m
SRPR = tan 30°
⇒ h10+h = 13√
⇒ 3–√ h = 10 + h
⇒ h = 103√−1×3√+13√+1 = 10(3√+1)2
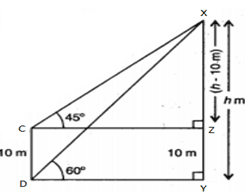
XYDY = tan 60°
hDY = 3–√
⇒ DY = h3√
XZCZ = tan 45°
∠RQS = 60° ∠PSQ = 30°
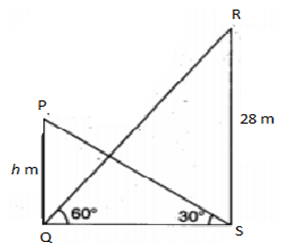
RSQS = tan 60°
27QS = 3–√
⇒ QS = 273√ …..(i)
PQQS = tan30°
⇒ hQS = 13√
⇒ 3–√ h = QS …..(ii)
3–√ h = 273√
⇒ h = 273 = 9 m
3. If the angle of elevation of the top of a hill from two points at distances p and q from the base and in the same straight line with it are complementary. Find the height of the hill.
Let PQ = h be the height of the hill,
QR = b, QS = a, such that ∠PSQ=θ

In rt. Δ PQS, we have
h = a tan θ …..(1)
In rt. Δ PQR, we have
h = b cot θ …..(2)
Multiplying (1) and (2), we get
4. From the figure, find the angle of depression of point Z from the point R.

5. Find the angle of elevation of the moon when the shadow of a tree h metres high is 3–√ h metres long.

The height of the pole be h m and length of its shadow is 3–√ h
Let θ be the elevation of the sun.
Consider rt.agl Δ ABC
tan θ = h3√h=13√
= tan 30°
6. A ladder 14 metres long just reaches the top of a wall. If the ladder makes an angle of 45° with the wall, find the height of the wall.
Here, length of the ladder is 14m and angle of elevation is 90°-45°=45°.
Let h m be the height of the wall

Consider rt.agl Δ PQR
h = 142√2 m
∴ The length of the wall is 72–√
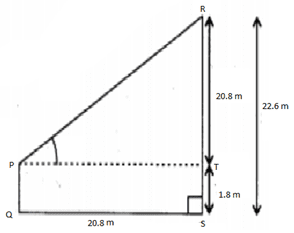
7. An observer 1.8 m tall is 20.8 m away from a tower 22.6 m high. Determine the angle of elevation of the top of the tower from the eye of the observer.

Here, PQ be the observer and RS be the tower of height 24 m.
PQ = TS = 1.8 m
RT = RS – TS
= 22.6 – 1.8
= 20.8 m
Now, Consider rt.agl ΔPTR, we have
1 = tan θ
tan 45° = tan θ
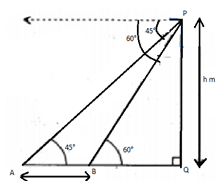
8.From a balloon vertically above a straight road, the angles of depression of two cars at an instant is found to be 45° and 60°. If the car are 100 m apart, find the height of the balloon.
Let the height of the balloon at P be h metres. Let A and B be the two cars. Thus, AB = 100m.

∠ PAQ= 45° and ∠ PBQ=60°
Now, Consider rt.agl ΔAQP,
Now, Consider rt.agl ΔPBQ,
h = 3–√h−3–√(100)
h = 3√(100)3√−1
h = 3√(100)3√−1 ×3√+13√+1
h = 3√(100)(3√+1)2
= 50(3+3–√)
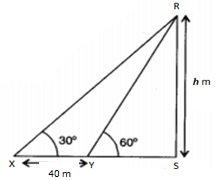
9. The shadow of a tower on a level surface is 40 m long when moon’s elevation is 30° then when it is 60°.Find the height of the tower.
XY=40 m, ∠RXS =30°, ∠RYS = 60°

Now, Consider rt.agl ΔRYS
Consider rt.agl ΔRXQ
3h = 403–√ + h
2h = 403–√
h = 203–√
∴ The height of the tower is 203–√ m
10. From the top of a tree h m high, the angle of depression of two objects, which are in the line with foot of the tree are γ and δ (δ > γ ). Find the distance between the two objects.
Let RS be the tree of height h m, X and Y are two objects such that

Now, Consider rt.agl ΔYSR
Now, Consider rt.agl ΔXSR
XY = h (cot γ + cot δ )
11. The angle of elevation of the top of a tower from two distinct points x and y from its foot are complementary. Prove that the height of the tower is xy−−√ .
Let h m be the height of the tower PQ. X and Y are two distinct points from its foot, such that PX = x and PY = y

Now, Consider rt.agl ΔXQP, we obtain
h = x tan θ …..(i)
Consider rt.agl ΔYQP, we obtain
h = y ×1tanθ …..(ii)
Multiply (I) and (ii), we get
h = xy−−√
∴ The height of the tower is xy−−√ .
12. The angle of elevation of the top of a tower from certain point at 30°. If the observer moves 10 m towards the tower, the angle of elevation of the top increases by 15° . Find the height of the tower.
Let h m be the height of the tower RS and P, Q are two points 10 m apaet, such that

Now, Consider rt.agl ΔQRS
Now, Consider rt.agl ΔPRS
(3–√−1 ) h = 10
∴ The height of the tower is 5(3–√ +1)
13. The angle of elevation of the top of a vertical tower from a point on the groung is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
Let XY be the vertical tower of height h m.
C and D are two points 10 m apart such that,

CD = ZY = 10 m ∠XCZ=45°and∠XBY=60°
XZ = XY – ZY = (h – 10) m
Consider rt.agl ΔDYX
Consider rt.agl ΔCZX
XZ = CZ
H – 10 = h3√
h (1−13√) = 10
h(3√−13√) = 10
h = 103√3√−1×3√+13√+1
= 103√3√−1×3√+13√+1
= 5(3 + 3–√ )m
14. The angle of elevation of the top of a tower 27 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and the height of the other tower.
Let us assume that PQ and RS be the two tower of height h m and 27 m respectively.

Consider rt.agl ΔRQS
Consider rt.agl ΔPSQ
From (i) and (ii), we have
From (ii), we get QS = 93–√ m
∴ The distance between two towers is 93–√ m and the height of the other tower is 9 m.
No comments:
Post a Comment